1 Find a Closed-form Solution to the Integral Equation Chegg

4. Applications of Derivatives

4.4 The Mean Value Theorem

Learning Objectives

Explain the meaning of Rolle's theorem.
Describe the significance of the Mean Value Theorem.
State three important consequences of the Mean Value Theorem.

The Mean Value Theorem is one of the most important theorems in calculus. We look at some of its implications at the end of this section. First, let's start with a special case of the Mean Value Theorem, called Rolle's theorem.

Rolle's Theorem

Informally, Rolle's theorem states that if the outputs of a differentiable function are equal at the endpoints of an interval, then there must be an interior point where $f\prime (c)=0.$ (Figure) illustrates this theorem.

Proof

Let We consider three cases:

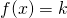for all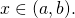 $x\in (a,b).$
There exists 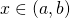$x\in (a,b)$ such that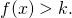
There exists 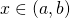$x\in (a,b)$ such that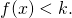

Case 1: If for all $x\in (a,b),$ then $f\prime (x)=0$ for all $x\in (a,b).$

Case 2: Since is a continuous function over the closed, bounded interval $\left[a,b\right],$ by the extreme value theorem, it has an absolute maximum. Also, since there is a point $x\in (a,b)$ such that the absolute maximum is greater than Therefore, the absolute maximum does not occur at either endpoint. As a result, the absolute maximum must occur at an interior point $c\in (a,b).$ Because has a maximum at an interior point and is differentiable at by Fermat's theorem, $f\prime (c)=0.$

Case 3: The case when there exists a point $x\in (a,b)$ such that is analogous to case 2, with maximum replaced by minimum.

□

An important point about Rolle's theorem is that the differentiability of the function is critical. If is not differentiable, even at a single point, the result may not hold. For example, the function is continuous over $\left[-1,1\right]$ and but $f\prime (c)\ne 0$ for any $c\in (-1,1)$ as shown in the following figure.

Let's now consider functions that satisfy the conditions of Rolle's theorem and calculate explicitly the points where $f\prime (c)=0.$

Using Rolle's Theorem

Verify that the function $f(x)=2{x}^{2}-8x+6$ defined over the interval $\left[1,3\right]$ satisfies the conditions of Rolle's theorem. Find all points guaranteed by Rolle's theorem.

Solution

The Mean Value Theorem and Its Meaning

Rolle's theorem is a special case of the Mean Value Theorem. In Rolle's theorem, we consider differentiable functions that are zero at the endpoints. The Mean Value Theorem generalizes Rolle's theorem by considering functions that are not necessarily zero at the endpoints. Consequently, we can view the Mean Value Theorem as a slanted version of Rolle's theorem ((Figure)). The Mean Value Theorem states that if is continuous over the closed interval $\left[a,b\right]$ and differentiable over the open interval then there exists a point $c\in (a,b)$ such that the tangent line to the graph of at is parallel to the secant line connecting and

Proof

The proof follows from Rolle's theorem by introducing an appropriate function that satisfies the criteria of Rolle's theorem. Consider the line connecting and Since the slope of that line is

$\frac{f(b)-f(a)}{b-a}$

and the line passes through the point the equation of that line can be written as

$y=\frac{f(b)-f(a)}{b-a}(x-a)+f(a).$

Let denote the vertical difference between the point and the point on that line. Therefore,

$g(x)=f(x)-\left[\frac{f(b)-f(a)}{b-a}(x-a)+f(a)\right]\text{.}$

Since the graph of intersects the secant line when and we see that Since is a differentiable function over is also a differentiable function over Furthermore, since is continuous over $\left[a,b\right],$ is also continuous over $\left[a,b\right].$ Therefore, satisfies the criteria of Rolle's theorem. Consequently, there exists a point $c\in (a,b)$ such that $g\prime (c)=0.$ Since

$g\prime (x)=f\prime (x)-\frac{f(b)-f(a)}{b-a},$

we see that

$g\prime (c)=f\prime (c)-\frac{f(b)-f(a)}{b-a}.$

Since $g\prime (c)=0,$ we conclude that

$f\prime (c)=\frac{f(b)-f(a)}{b-a}.$

□

In the next example, we show how the Mean Value Theorem can be applied to the function $f(x)=\sqrt{x}$ over the interval $\left[0,9\right].$ The method is the same for other functions, although sometimes with more interesting consequences.

Verifying that the Mean Value Theorem Applies

One application that helps illustrate the Mean Value Theorem involves velocity. For example, suppose we drive a car for 1 h down a straight road with an average velocity of 45 mph. Let and denote the position and velocity of the car, respectively, for $0\le t\le 1$ h. Assuming that the position function is differentiable, we can apply the Mean Value Theorem to conclude that, at some time $c\in (0,1),$ the speed of the car was exactly

$v(c)={s}^{\prime }(c)=\frac{s(1)-s(0)}{1-0}=45\text{mph}.$

Mean Value Theorem and Velocity

Suppose a ball is dropped from a height of 200 ft. Its position at time is $s(t)=-16{t}^{2}+200.$ Find the time when the instantaneous velocity of the ball equals its average velocity.

Solution

$\frac{5}{2\sqrt{2}}$ sec

Corollaries of the Mean Value Theorem

Let's now look at three corollaries of the Mean Value Theorem. These results have important consequences, which we use in upcoming sections.

At this point, we know the derivative of any constant function is zero. The Mean Value Theorem allows us to conclude that the converse is also true. In particular, if ${f}^{\prime }(x)=0$ for all in some interval then is constant over that interval. This result may seem intuitively obvious, but it has important implications that are not obvious, and we discuss them shortly.

Key Concepts

1. Why do you need continuity to apply the Mean Value Theorem? Construct a counterexample.

2. Why do you need differentiability to apply the Mean Value Theorem? Find a counterexample.

Solution

One example is $f(x)=|x|+3,-2\le x\le 2$

3. When are Rolle's theorem and the Mean Value Theorem equivalent?

4. If you have a function with a discontinuity, is it still possible to have ${f}^{\prime }(c)(b-a)=f(b)-f(a)?$ Draw such an example or prove why not.

Solution

Yes, but the Mean Value Theorem still does not apply

For the following exercises, determine over what intervals (if any) the Mean Value Theorem applies. Justify your answer.

5. $y= \sin (\pi x)$

6. $y=\frac{1}{{x}^{3}}$

Solution

$(\text{−}\infty ,0),(0,\infty )$

7. $y=\sqrt{4-{x}^{2}}$

8. $y=\sqrt{{x}^{2}-4}$

Solution

$(\text{−}\infty ,-2),(2,\infty )$

9. $y=\text{ln}(3x-5)$

For the following exercises, graph the functions on a calculator and draw the secant line that connects the endpoints. Estimate the number of points such that ${f}^{\prime }(c)(b-a)=f(b)-f(a).$

10. [T] $y=3{x}^{3}+2x+1$ over $\left[-1,1\right]$

11. [T] $y= \tan (\frac{\pi }{4}x)$ over $\left[-\frac{3}{2},\frac{3}{2}\right]$

12. [T] $y={x}^{2} \cos (\pi x)$ over $\left[-2,2\right]$

13. [T] $y={x}^{6}-\frac{3}{4}{x}^{5}-\frac{9}{8}{x}^{4}+\frac{15}{16}{x}^{3}+\frac{3}{32}{x}^{2}+\frac{3}{16}x+\frac{1}{32}$ over $\left[-1,1\right]$

For the following exercises, use the Mean Value Theorem and find all points such that $f(2)-f(0)={f}^{\prime }(c)(2-0).$

14. $f(x)={x}^{3}$

Solution

$c=\frac{2\sqrt{3}}{3}$

15. $f(x)= \sin (\pi x)$

16. $f(x)= \cos (2\pi x)$

Solution

$c=\frac{1}{2},1,\frac{3}{2}$

17. $f(x)=1+x+{x}^{2}$

18. $f(x)={(x-1)}^{10}$

Solution

19. $f(x)={(x-1)}^{9}$

For the following exercises, show there is no such that $f(1)-f(-1)={f}^{\prime }(c)(2).$ Explain why the Mean Value Theorem does not apply over the interval $\left[-1,1\right].$

20. $f(x)=|x-\frac{1}{2}|$

Solution

Not differentiable

21. $f(x)=\frac{1}{{x}^{2}}$

22. $f(x)=\sqrt{|x|}$

Solution

Not differentiable

For the following exercises, determine whether the Mean Value Theorem applies for the functions over the given interval $\left[a,b\right].$ Justify your answer.

24. $y={e}^{x}$ over $\left[0,1\right]$

25. $y=\text{ln}(2x+3)$ over $\left[-\frac{3}{2},0\right]$

26. $f(x)= \tan (2\pi x)$ over $\left[0,2\right]$

Solution

The Mean Value Theorem does not apply since the function is discontinuous at $x=\frac{1}{4},\frac{3}{4},\frac{5}{4},\frac{7}{4}.$

27. $y=\sqrt{9-{x}^{2}}$ over $\left[-3,3\right]$

28. $y=\frac{1}{|x+1|}$ over $\left[0,3\right]$

29. $y={x}^{3}+2x+1$ over $\left[0,6\right]$

30. $y=\frac{{x}^{2}+3x+2}{x}$ over $\left[-1,1\right]$

Solution

The Mean Value Theorem does not apply; discontinuous at

31. $y=\frac{x}{ \sin (\pi x)+1}$ over $\left[0,1\right]$

32. $y=\text{ln}(x+1)$ over $\left[0,e-1\right]$

33. $y=x \sin (\pi x)$ over $\left[0,2\right]$

34. over $\left[-1,1\right]$

Solution

The Mean Value Theorem does not apply; not differentiable at

For the following exercises, consider the roots of the equation.

35. Show that the equation $y={x}^{3}+3{x}^{2}+16$ has exactly one real root. What is it?

36. Find the conditions for exactly one root (double root) for the equation $y={x}^{2}+bx+c$

Solution

$b=\text{±}2\sqrt{c}$

37. Find the conditions for $y={e}^{x}-b$ to have one root. Is it possible to have more than one root?

For the following exercises, use a calculator to graph the function over the interval $\left[a,b\right]$ and graph the secant line from to Use the calculator to estimate all values of as guaranteed by the Mean Value Theorem. Then, find the exact value of if possible, or write the final equation and use a calculator to estimate to four digits.

38. [T] $y= \tan (\pi x)$ over $\left[-\frac{1}{4},\frac{1}{4}\right]$

Solution

$c=\text{±}\frac{1}{\pi }{ \cos }^{-1}(\frac{\sqrt{\pi }}{2}),$ [latex]c=\text{±}0.1533[/latex]

39. [T] $y=\frac{1}{\sqrt{x+1}}$ over $\left[0,3\right]$

40. [T] $y=|{x}^{2}+2x-4|$ over $\left[-4,0\right]$

Solution

The Mean Value Theorem does not apply.

41. [T] $y=x+\frac{1}{x}$ over $\left[\frac{1}{2},4\right]$

42. [T] $y=\sqrt{x+1}+\frac{1}{{x}^{2}}$ over $\left[3,8\right]$

Solution

$\frac{1}{2\sqrt{c+1}}-\frac{2}{{c}^{3}}=\frac{521}{2880};$ [latex]c=3.133,5.867[/latex]

43. At 10:17 a.m., you pass a police car at 55 mph that is stopped on the freeway. You pass a second police car at 55 mph at 10:53 a.m., which is located 39 mi from the first police car. If the speed limit is 60 mph, can the police cite you for speeding?

44. Two cars drive from one spotlight to the next, leaving at the same time and arriving at the same time. Is there ever a time when they are going the same speed? Prove or disprove.

1 Find a Closed-form Solution to the Integral Equation Chegg

Source: https://opentextbc.ca/calculusv1openstax/chapter/the-mean-value-theorem/

Keegan Bacipte

1 Find a Closed-form Solution to the Integral Equation Chegg

4.4 The Mean Value Theorem

Learning Objectives

Rolle's Theorem

Proof

Using Rolle's Theorem

Solution

The Mean Value Theorem and Its Meaning

Proof

Verifying that the Mean Value Theorem Applies

Mean Value Theorem and Velocity

Solution

Corollaries of the Mean Value Theorem

Key Concepts

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Menu Halaman Statis